The hecking fuck, nothing's working. What arcane combination of symbols must I arrange to make media queries work on my phone. Sometime it works, but not actually. The documentation and articles made it sound easy, but the sample codes doesn't even work. Then again, maybe it's just my phone's outdated browser.
I give up, doing calculus suddenly seemed way more easier when trying to make mobile responsive frontend.
There, fixed bugs, and looking good. I want to finish on working on the mobile view so I could test it in the phone before the week ends.
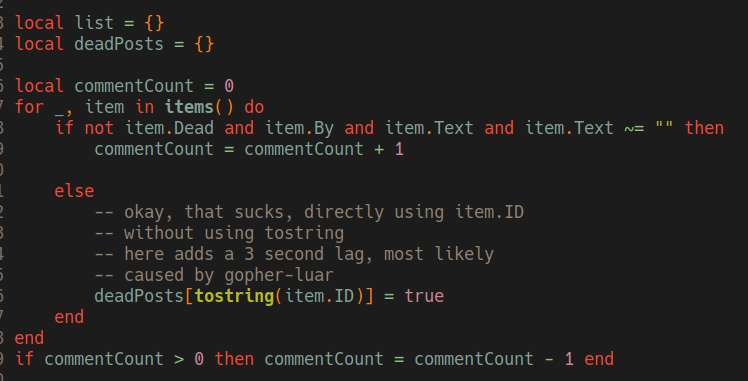
Worked on SN, I fixed several bugs. I also found out that using a field mapped by gopher-luar as a table key causes several seconds of lag. I'm not really why is that, but it's a massive wtf. The fix is to cast the ID first to string before using it as an index.
Also another blocker is the mouseover event. It seems that just moving my mouse inside an element causes the mouseout to emit repeatedly.
Aha, nevermind, fixed it. The bug seems to happen when I nest small elem inside a link: | <a><small>...</small></a> Removing the small fixes the bug. Once again, not sure why would that be a bug in the first place.
Oh well, this is one buggy friday.
So the book did actually and directly used product and power rule for the quotient rule. The approach I did was to start with y = uv~ and get the derivative. But then I wondered, what variable is ∆u and ∆v dependent on? The book used the following notation:
| y = uv | y + ∆y = (u + ∆u)(v + ∆v)
If I let u = w~, how would that affect ∆u? Will it be ∆u~?
Once again, I see and hated the implicit handwavy notations that mathematicians use. I tried explicity converting dependent variables to functions, but then I didn't do any better, it's actually more verbose:
let Y(x) = U(x)V(x)
let ∆Y(x, ∆x) = U(x + ∆x)V(x + ∆x) - U(x)V(x)
= [U(x) + U(∆x)][V(x) + V(∆x)] - U(x)V(x)
= (u + ∆u)(v + ∆v) - uv
where
u = U(x)
v = V(x)
∆u = U(∆x)
∆v = V(∆x)
let Y(x) = U(x)V(x)~
let ∆Y(x) = (u + ∆u)(v~ + ∆v~) - uv~